MUNDO DE LA GEOMETRIA: 2012

domingo, 25 de noviembre de 2012

taketina

taketina: es un proceso en grupo, singular y musical. Actividad el potencial musical y humano a través del ritmo, la enseñanza de taketina abre a cada persona la puerta a su talento rítmico.la taketina ofrece. la compresion ritmica y la creatividad en todos los estilos de musiva.
facilitar la compresión de voz orientación rítmica y la creatividad en todos los estilos de musica.
video de la taketina

sábado, 24 de noviembre de 2012

Filosofos y matemàticos (musicos)

euclides : uno de los mas grades matemáticas de la época antigua fue el primero que estableció el método de la demostración de la geometría. por un punto exterior a una recta solo puede trazarse una prepenticular a la misma y solo una.

arquitas de tarento: (430 a.c- 360 a.c) pretenecio a los pitagóricos, alumno de la escuela de filolao de crotona fue amigo de planton a el que conoció duarante el primer viaje que este realizo a el sur de Italia tras la muerte de socrates en su carta séptima planton le asegura que arquitas trato de rescatarlo en sus dificultades con dionisioll de siracusa mediante una carta de recomenacion y enviando un barco a sicilia en 361 a.c para algunos autores fue el maestro pitagorico de planton y para otros su discípulo.

carl friedrich gauss: (30 de abril del 1777-23 de febrero 1855) fue un matemático, astrónomo y fisco alemán teniendo una infecten . considerado como el príncipe de las matemáticas y el matemático mas grande de la antigüedad. ha tenido una influencia notable en muchos campos de la matemática y de la ciencia y es considerado uno de los matemáticos que a tenido mas influencia con las matemáticas en la historia.

historia de la musica

historia de la música: la música comienza en prehistoria. Dado que toda cultura conocida ha tenido alguna forma de manifestación musical, la historia dela música abarca a todas las sociedades y épocas, y no se limita, como ha venido siendo habitual a occidente, donde se ha utilizado la expresión. la música de una cultura esta estrechamente relacionada con otros aspectos de la cultura como la organización económica el desarrollo técnico la actitud de los compositores y su relación con los oyentes las ideas estéticas mas generalizadas de cada comunidad la visión acerca de la función del arte en la sociedad así como las variantes biográficas de cada autor.
vídeo sobre la historia de la musica:

Definición de Triángulo

triángulos:Es un polingono determinado por tres rectas que se cortan dos a dos entres, por lo tanto, un triangulo tiene 3 ángulos interiores,3 ángulos interiores, 3 lados y 3 vértices.
*de acuerdo con sus lados, los triángulos se clasifican así:
triangulo equilatero
triangulo isósceles
triangulo escaleno
* de acuerdo con la medida sus ángulos, los triángulos se clasifican así:
triangulo acutángulo
triangulo rectángulo
triangulo obtusángulo
triangulo isósceles
triangulo equiangulo

vídeo sobre las clases de triángulos:

Definición Ley del Seno y Ley del Coseno

ley del seno:

la ley de seno es una relación de tres igualdades que siempre se cumple entre los lados y ángulos de un triangulo cualquiera, y que es útil para resolver ciertos tipos de problemas de triángulos

la ley de seno dice así:

la ley de coseno:

La ley de cosenos se puede considera como una extencion de el teorema de pitagoras aplicable a todos los triángulos. Ella enuncia así: el cuadrado de un la de un triangulo es igual a la suma de los cuadrados de los otros dos lados menos el doble producto de estos dos lados multiplicando por el coseno del angulo que forman

si aplicamos este teorema al triangulo.

historia de grecia

historia de Grecia: La civilización helénica de la Grecia antigua se extendió por la península balcanica, las islas del mar egeo y las costas de la península de antolia, en la actual Turquía, constituyendo la llamada helade. La civilización helénica o griega tiene su origen en las culturas cretense y micenica. Hacia el 2700 a.c se desarrollo en la isla creta una rica y floreciente cultura comercial perteneciente a la edad del bronce. Esta cultura recibe el nombre de minoica o cretense, en torno al año 1600 a.c los aqueos, un pueblo de habla griega y de origen indoeuropeo, irrumpieron en el territorio de Grecia continental, estableciéndose en el extremo noreste de la península del peloponeso. Este pueblo llego a dominar a los cretenses. su cuidad mas importante fue micenas. Hacia el año 1200 a.c otro pueblo de origen griego, los dorios que utilizaba armas de hierro, se apoderaron de Grecia derrotando a los micenios. La guerra de troya, descrita por Homero en la Iliada, fue, probablemente uno de los conflictos bélicos que tuvieron relación con esta invasión. Esparta y corinto se transformaron en los principales ciudades dóricas con los dorios empenzo un periodo de retroceso cultural que se conoce con el nombre de edad oscura.
vídeo sobre la historia de grecia:

BIOGRAFIA DE ARQUIMEDES

BIOGRAFÍA DE ARQUIMEDES:
*ARQUIMEDES: (287 a.c -212 a.c) fue un matemático griego fisco, ingeniero, inventor y astrónomo. aunque se conocen pocos detalles de su vida , es considerado como uno de los científicos mas importantes, de la antigüedad clásica entre sus avances en la fisca. uso el método exhaustivo para calcular el área bajo el arco
de una parábola con el sumatorio de una serie infinita y dio una aproximación extremadamente precisa de numero pi.

vídeo sobre la vida de arquimedes:

INVENTOS DE ARQUIMEDES

INVENTOS DE ARQUIMDES:
1. la garra de arquimedes: la garra de arquimedes es una arma que fue diseñada para poder defender a la cuidad de siracusa del asedio al que la que habían sometido los romanos. También conocida como el agitador de barcos, la garra consistía en un brazo semejante ala grúa de donde esta suspendido un enorme gancho de metal. Cuando se dejaba caer la garra sobre un barco enemigo el brazo se balancearía en sentido ascendente, levantando el barco fuera del agua y posiblemente hundiéndolo.

EL TORNILLO DE ARQUIMEDES: El tronillo de arquimedes ( superficie, helicoidal que rodea a un cilindro) dentro de un tubo.La invención de este tornillo se le atribuye al pensador griego arquimedes de siracusa en el siglo tercero. El supuesto de que esta atribucion fuera realizada en el siglo sexto antes de cristo por la ley babilonio nabucondonosor, por el dalley helenistico fue refutada por la falta de evidencia literaria y arqueología del tornillo antes del 250 a.c .

vídeo sobre el tornillo de arquimedes:

principio de arquimedes: Cuenta como invento un método para determinar el volumen de un objecto con una forma irregular.

el rayo de calor de arquimedes: según la tradición, dentro de sus trabajos en la defensa de siracusa sin embargo, las fuentes que recogen estos hechos son tardías, siendo la primera de ellas galeno, ya en el siglo ll, luciano de samosata historiador tambien en el siglo ll escribió que durante el sitio de siracusa (213-211 a.c) arquimedes repelió un ataque llevado a cabo por soladados romanos con fuego. siglos mas tarde, antemio de tralles menciona los espejos ustorios como arma utilizada de arquimedes.

viernes, 23 de noviembre de 2012

graficas y funciones trigonometricas

FUNCIONES TRIGONOMÉTRICAS (concepto, historia, gráficas):

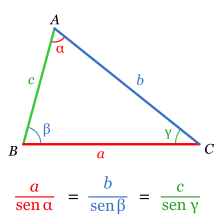
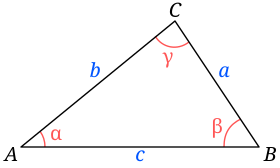
En trigonometria se define como la razón entre cateto opuesto y la hipotenusa, el astrónomo y matemático hindú (476-550 d.c) estudio el concepto de seno, cuando los escritores árabes tradujeron estas obras científicas al árabe se referían a el termino sánscrito como jiba sin embrago, en el árabe escrito se omiten las vocales, por lo que el termino quedo abreviado, escritores posteriores que no sabían el origen del extrajeron de ka palabra creyeron que jb era la abreviatura de jiab( que quiere decir bahia) a finales del siglo xll el traductor italiano gherardk el cremona (1114-1187) tradujo estos escritos del árabe latin reemplazo el insensato jiab por si contraparte latina sinus ( hueco, cavidad , bahia) luego ese sinus se convirtió en el español seno

pasos para construir la función seno:

* cateto opuesto y la hipotenusa

*como la ordena correspondiente a un punto que pertenece a una circunferencia unitaria centrada en el origen (c=1)

en la siguiente imagen se puede ver la función seno desarrollada en geogebra:

función contangente: la función cotagente se define como cateto adyacente y cateto adyacente 1/tan

en la siguiente imagen se puede ver la imagen de la funcion contangente:

función coseno: en trrigonometria el coseno de un angulo agudo en un triangulo rectagulo se define como la razón entre cateto adyacente a es angulo y la hipotenusa

en la siguiente imagen se muestra la funcion coseno:

funciona tangente: se aplica ala linea o superficie que se toca en un único punto con otra linea o superficie sin llegar a otra

pasos para realizar la función tangente

en la siguiente imagen se muestra la función tangente:

función cosecante: es la razón trigonométrica inversa del seno on también su inverso sustantivo

en la siguiente imagen se puede ver como es la función cosecante:

función secante: es la razón trigonométrica inversa a el coseno o también su inverso multiplicativo:

en la siguiente imagen se obsereva la función secante:

jueves, 31 de mayo de 2012

Funciones Trigonometricas

SENO:

COSENO:

TANGENTE:

COTANGENTE:

SECANTE:

COSECANTE:

miércoles, 28 de marzo de 2012

5.4 Teorema del Seno y Coseno

TEOREMA DEL SENO: Es una relaciones de la proporcionalidad entres longitudes de los lados de un triangulo y los senos de los anguilos respectivamente opuestos. si en un triangulo A,B,C las medidas de los lados opuestos a los angulos A,B,C son respectivamente a,b,c entonces

$\frac{a}{\operatorname{sen}\,A} =\frac{b}{\operatorname{sen}\,B} =\frac{c}{\operatorname{sen}\,C}$

TEOREMA DEL COSENO: Es una genarazacion del teorema de pitagoras en los triángulos no rectángulos que se utiliza normalmente en trigonometria.
dado un triagulo A,B,C siendo α, β, y , los angulos y, a,b,c los lados respectivamente opuestos

$c^2=a^2+b^2-2ab\,\cos(\gamma)$

5.3 Relaciones Trigonometricas

Consideremos el triángulo rectángulo ABC:
El ángulo α cumple que: $sen α$ = b a y $\cos =$ c a .

Elevamos al cuadrado ambas expresiones: $sen$ 2 α = b 2 a 2 y $\cos$ 2 α = c 2 a 2 , y las sumamos: $sen$ 2 α +cos 2 α = b 2 a 2 + c 2 a 2 = b 2 + c 2 a 2 = a 2 a 2 = 1 . Luego,

sen² α + cos² α = 1

La expresión anterior se conoce como relación fundamental de la trigonometría.
Otra relación importante es:
$tg α$ = sen α cos α

Comprobamos esta relación dividiendo:

$sen α$ cos α = b a c a = b · a c · a = b c = tg α
A partir de la relación fundamental de la trigonometría se pueden obtener otras dos relaciones, dividiendo los dos miembros de la relación fundamental por cos² α y sen² α:
$sen$ 2 α

5.2 Teorema de Pitagoras

PROBLEMA: una casa tiene 120m de largo y 80m de ancho ¿cual es la longitud de la casa diagonal de la casa

teorema de pitagoras

este teorema se usa en los triángulos rectángulos.

el cuadrado de la hipotenusa es igual a la suma de los catetos:

5.1 Historia de la trigonometria

HISTORIA DE LA TRIGONOMETRIA: Los babilonios determinaron aproximaciones de medidas de angulos o de longitudes de los triángulos rectángulos. varias tablas grabadas sobre arcilla seca lo testimonian así por ejemplo, una tablilla babilonia escrita en cueneiforme denominada plimpton 322 ( en torno al 1900 a. c) muestras quince ternas pitagoracas

4.5 Triangulo Acutangulo

TRIANGULO ACUTÁNGULO: Cuando sus 32 angulos interiores son menores de 90º.

4.4 Triangulo Rectangulo

TRIANGULO RECTÁNGULO: Es el que tiene un angulo de 90º.

4.3 Triangulo Escaleno

TRIANGULO ESCALENO: Es el que no tiene todos sus ángulos diferentes.

4.2 Triangulo Isoceles

TRIANGULO ISÓSCELES: Tiene 2 lados iguales, estableciendo así una relación entre longitudes y ángulos.

4.1 Triangulo Equilatero

TRIANGULO EQUILATERO: Es el que tiene sus 3 lados y sus ángulos iguales.

3.3 Nombres de Algunos Pilogonos

Triangulo
Cuadrilatero
Pentagono
Hexagono
Heptagono
Octagono
Nonagono
Decagono
Endecagono
Tridecagono
Tetradecagono
Pentadecagono
Hexadecagono
Heptadecagono
Octadecagono
Eneadecagono
Icosagono
Triacontagono
Tetracontagono
Pentacontagono
Hexacontagono
Heptacontagono
Octacontagono